傅里叶变换性质公式的理解

197次浏览发布时间：2024-05-16 13:50:29

傅里叶变换本质及其公式解析

傅里叶变换的本质傅里叶变换的公式为

傅里叶变换公式

可以把傅里叶变换也成另外一种形式：

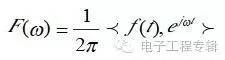
内积表达式

可以看出，傅里叶变换的本质是内积，三角函数是完备的正交函数集，不同频率的三角函数的之间的内积为0，只有频率相等的三角函数做内积时，才不为0。

下面从公式解释下傅里叶变换的意义因为傅里叶变换的本质是内积，所以f(t)和

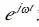
求内积的时候，只有f(t)中频率为的分量W才会有内积的结果，其余分量的内积为0。可以理解为f(t)在

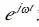
上的投影，积分值是时间从负无穷到正无穷的积分，就是把信号每个时间在w的分量叠加起来，可以理解为f(t)在

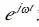
上的投影的叠加，叠加的结果就是频率为的分量，也就形成了频谱。傅里叶逆变换的公式为

下面从公式分析下傅里叶逆变换的意义傅里叶逆变换就是傅里叶变换的逆过程，在和求内积的时候，只有t 时刻的分量内积才会有结果，其余时间分量内积结果为0，同样积分值是频率从负无穷到正无穷的积分，就是把信号在每个频率在t时刻上的分量叠加起来，叠加的结果就是f(t)在t时刻的值，这就回到了我们观察信号最初的时域。对一个信号做傅里叶变换，然后直接做逆变换，这样做是没有意义的，在傅里叶变换和傅里叶逆变换之间有一个滤波的过程。将不要的频率分量给滤除掉，然后再做逆变换，就得到了想要的信号。比如信号中掺杂着噪声信号，可以通过滤波器将噪声信号的频率给去除，再做傅里叶逆变换，就得到了没有噪声的信号。

优点：频率的定位很好，通过对信号的频率分辨率很好，可以清晰的得到信号所包含的频率成分，也就是频谱。

缺点：因为频谱是时间从负无穷到正无穷的叠加，所以，知道某一频率，不能判断，该频率的时间定位。不能判断某一时间段的频率成分。