偶函数定义是什么（函数的奇偶性及相关题型）
100次浏览
发布时间：2024-11-06 08:32:21
函数奇偶性的定义（必修一P104）：偶函数关于Y轴对称；奇函数关于原点对称。
奇偶性的判断：注意第一个是关于顶点并非原点。
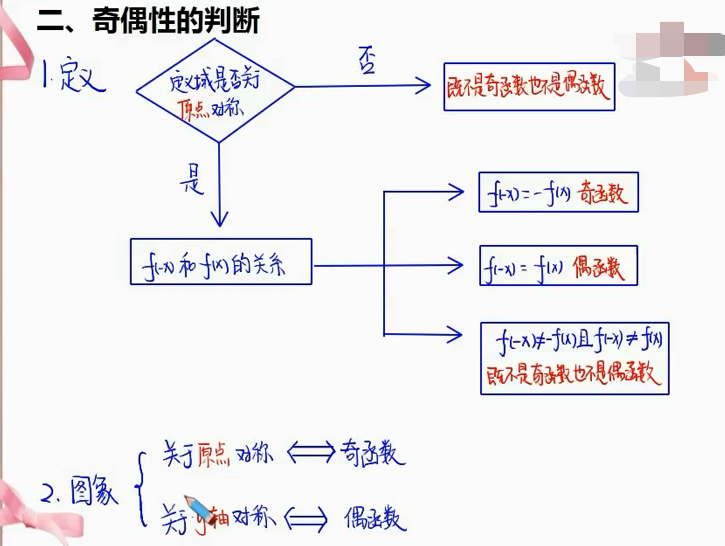
奇偶函数相加或相减，教材上说奇偶性未定。只有一个特例，y=0。它既可以是奇函数也可以是偶函数也可以既是奇函数又是偶函数。但是在高考考题里，奇偶函数相加或相减的答案就是既不是偶函数也不是奇函数。
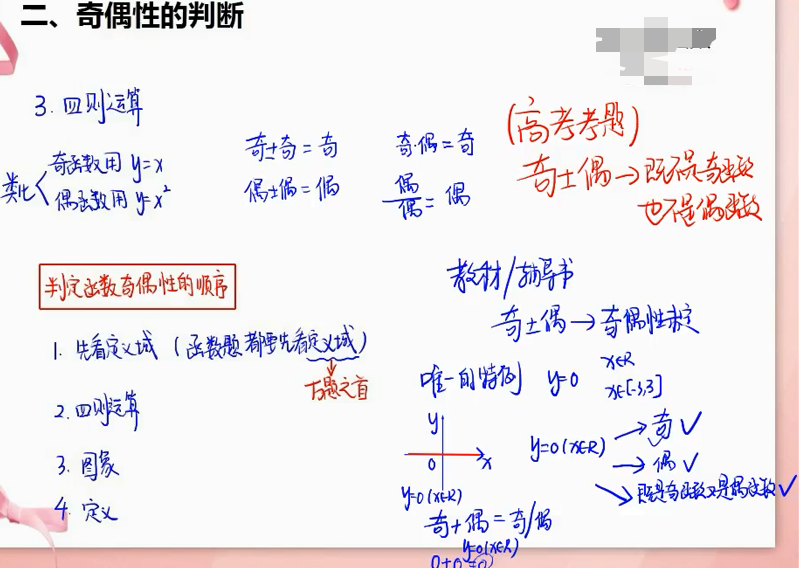
判断奇偶函数首先看定义域。
判断奇偶性例题1：利用定义法判断函数的奇偶性。
无论是奇函数还是偶函数，无论对Y值还是定义域X值加绝对值，那么结果就是偶函数。
考察:奇函数加减偶函数等于即不是奇函数也不是偶函数。
既不是奇函数也不是偶函数的题型，就借助来过渡。
重要！
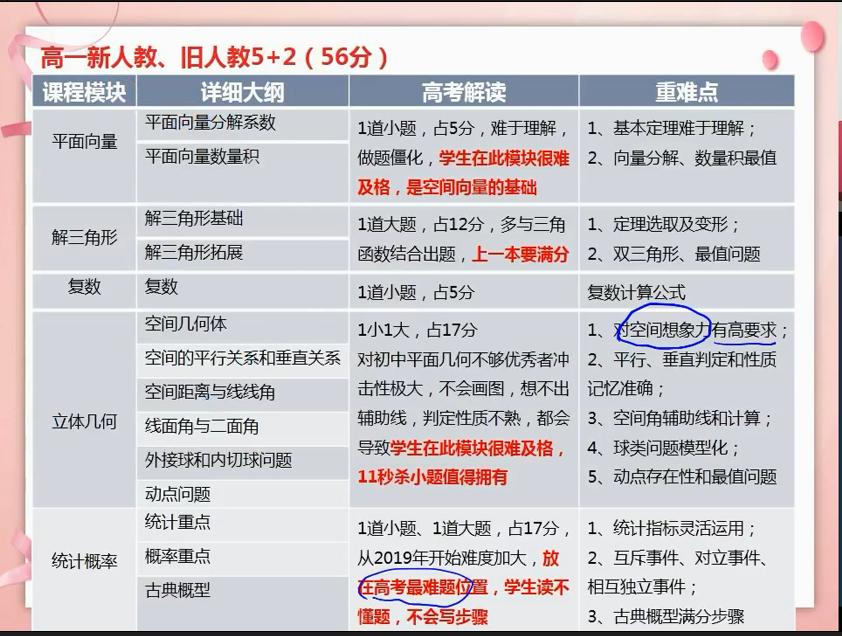
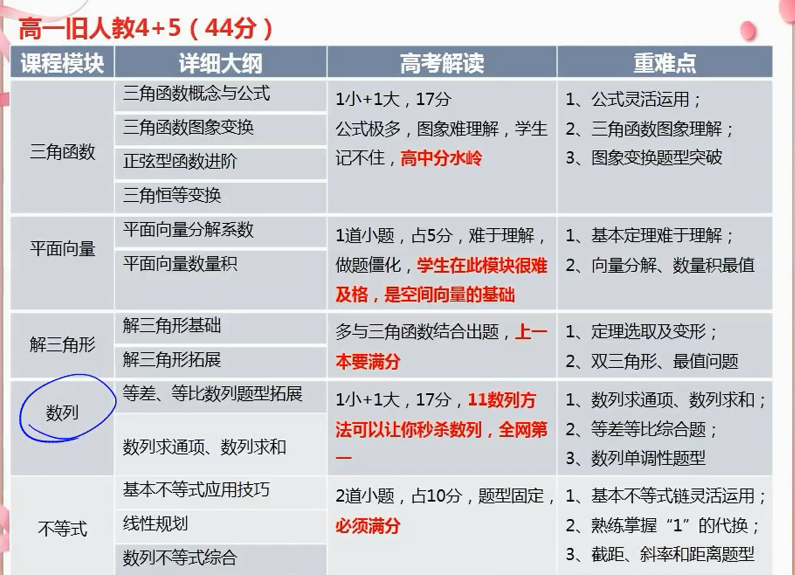
例题：机场函数：奇函数加减常数。第一种利用gx函数过渡。第二种利用三步法（核心是奇函数的性质，关于中心对称见讲义）。
三步法应用：
如果奇函数的定义包含0，则f0一定等于0。
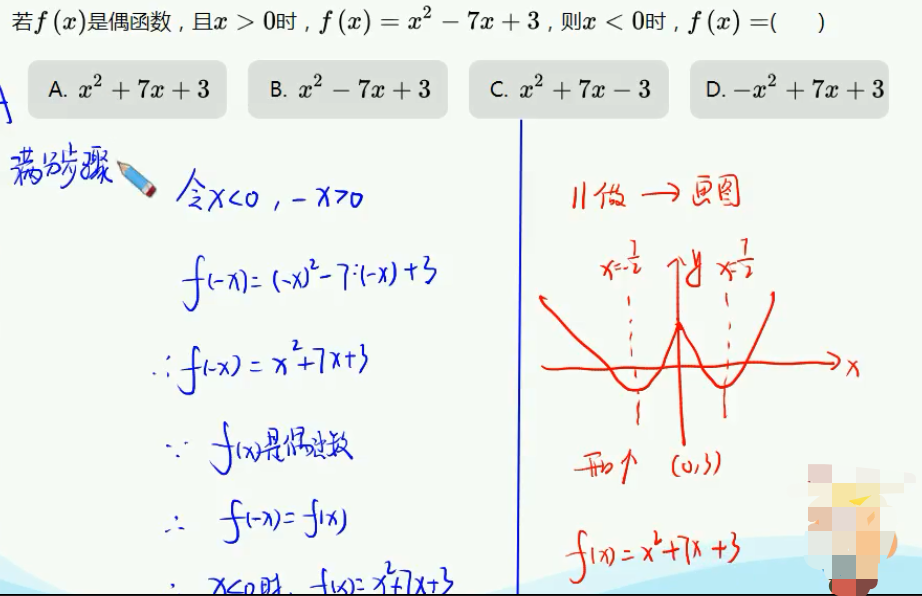
善用函数的图形结合。
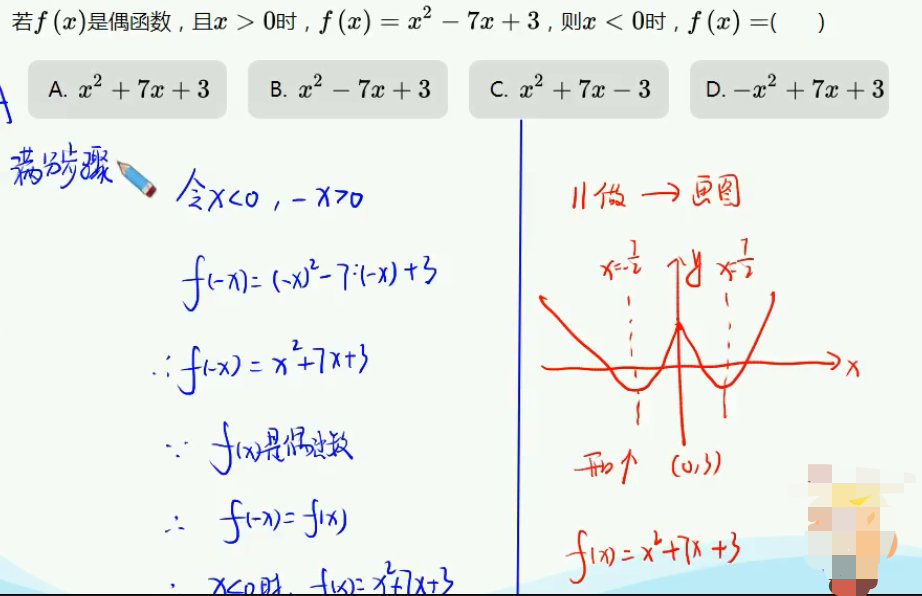
满分步骤：
题型考察：奇偶性与单调性结合的情况时，先考虑奇偶性再用单调性。两种题型。
考察题：
相关文章
中国电影影人榜（中国电影史上票房最高的十位演员）
2024-11-06 11:15:08
羊油怎么吃才好吃（好吃到流泪的蒸油香，连吃三天都不够）
2024-11-06 11:00:21
espana是哪个国家（盘点欧洲17个最美丽的广场 你去过哪几个？）
2024-11-06 10:32:39
南海在哪里具体位置（我国的南海到底有多大您知道吗？）
2024-11-06 10:17:35
榆社县属于哪个市（中国县城概况：榆社！）
2024-11-06 10:02:27
资格后审如何操作（资格后审如何实现？）
2024-11-06 09:47:24